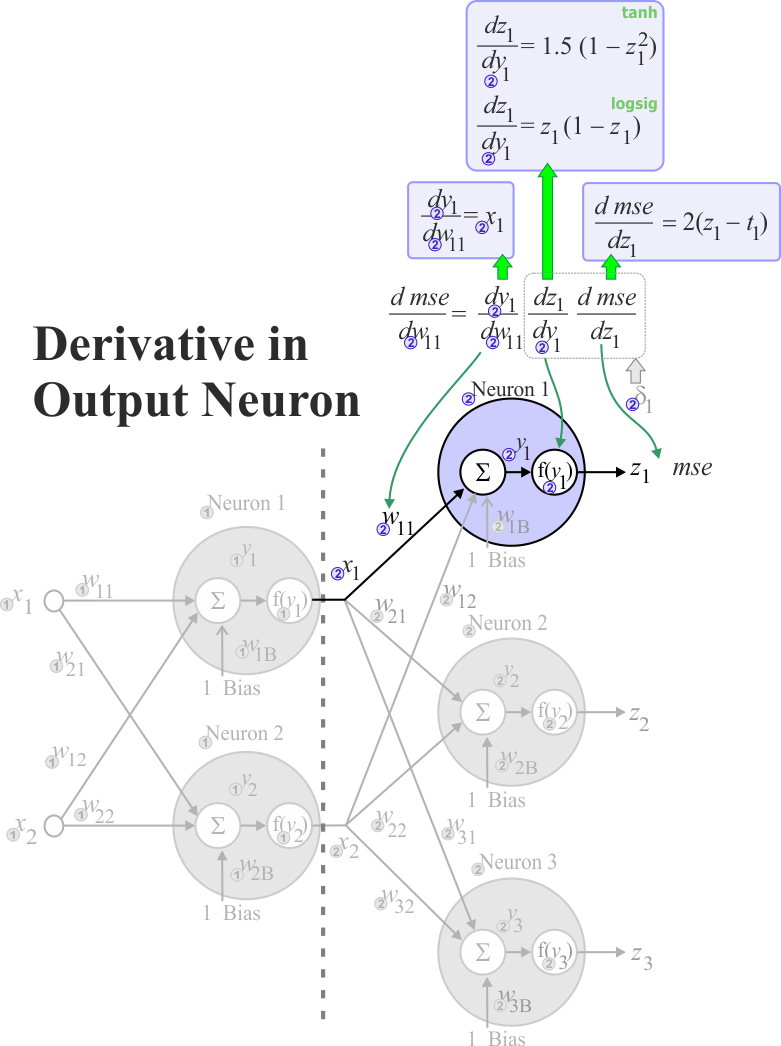
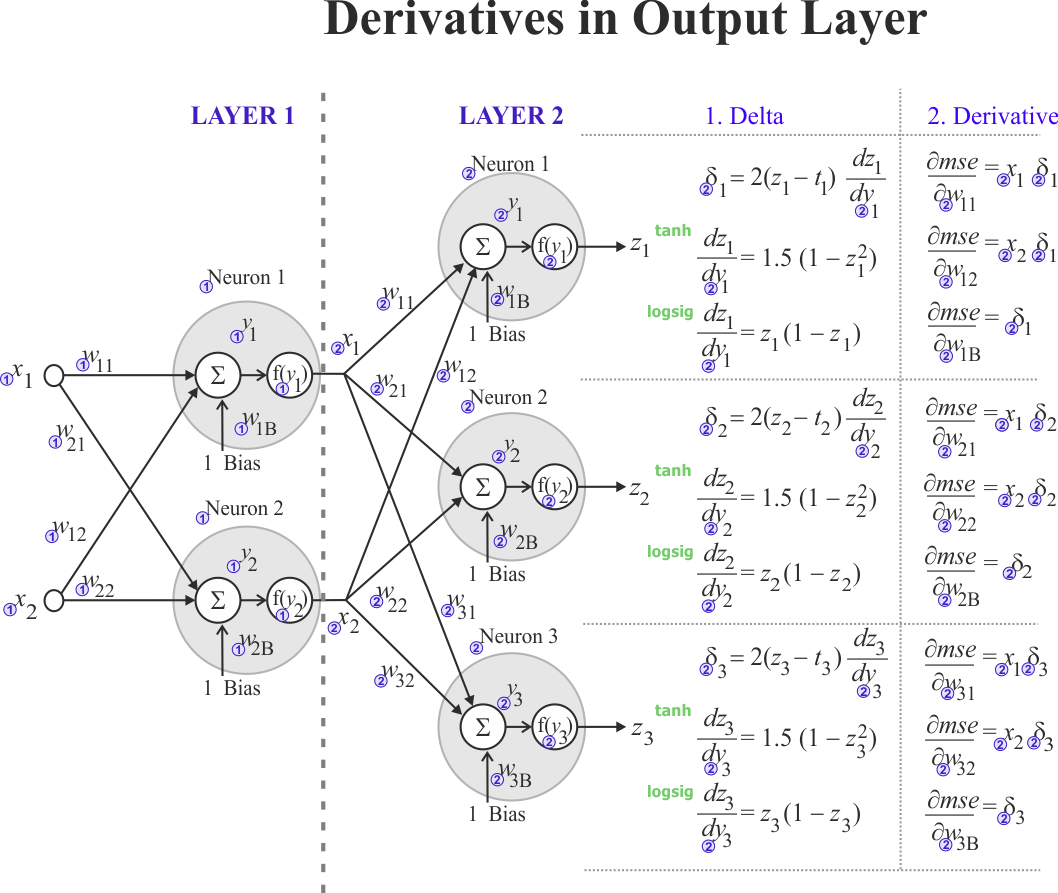
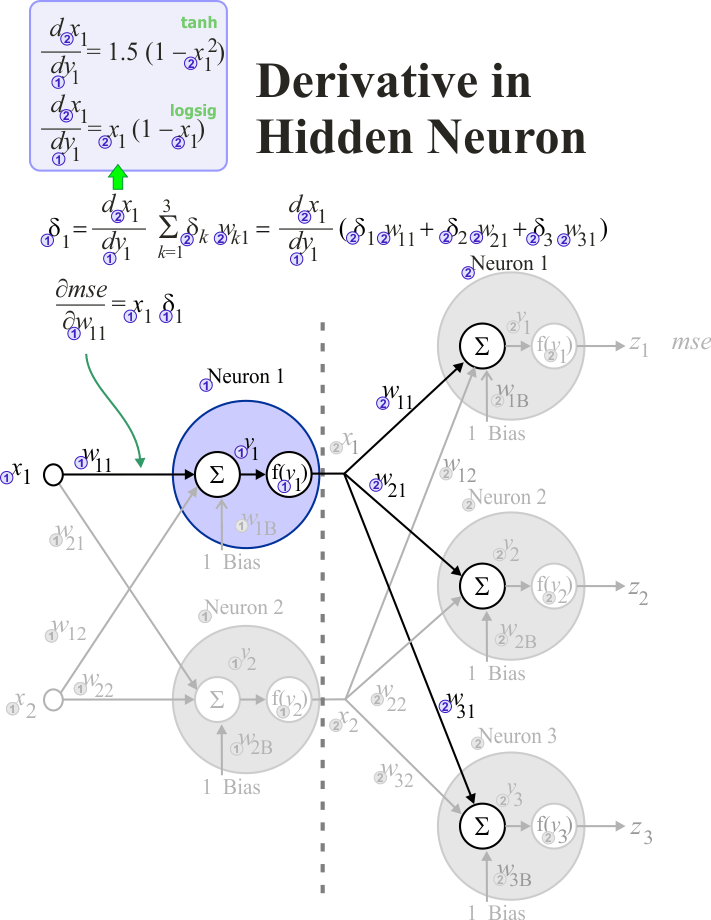
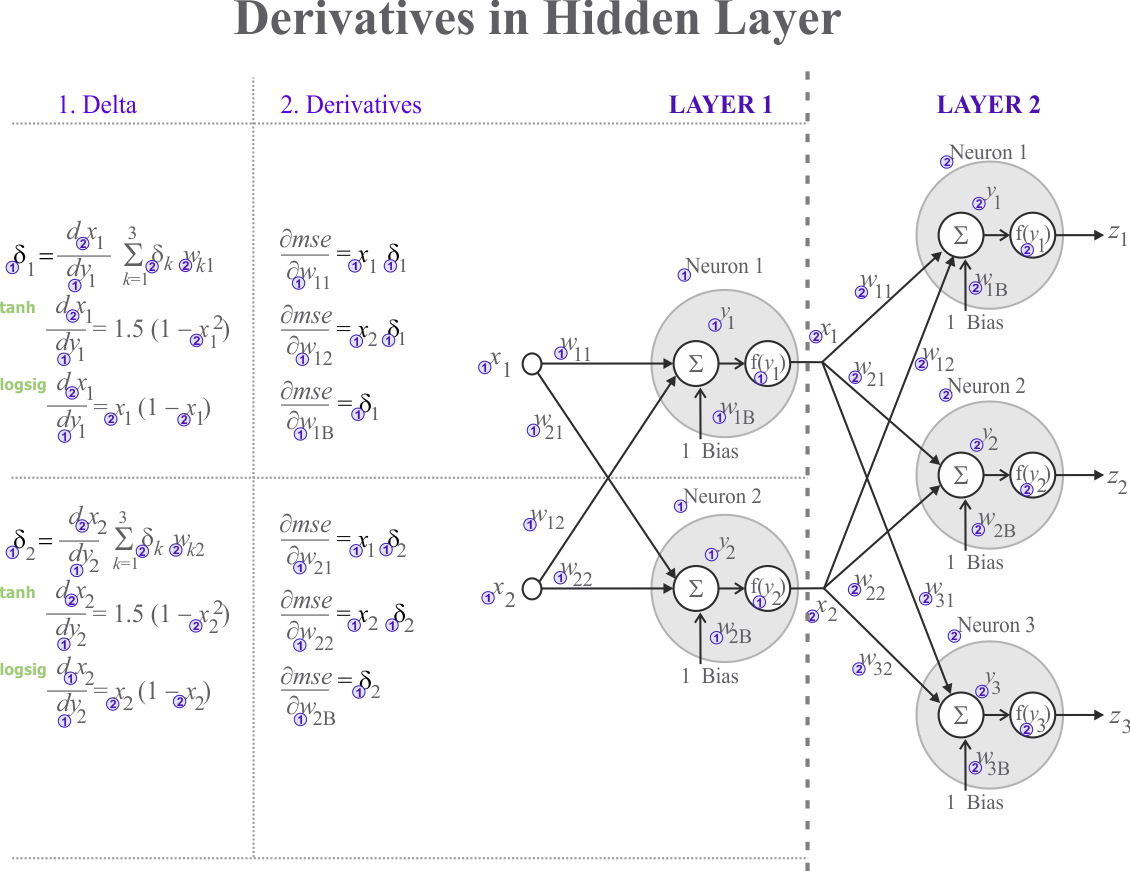
In order to compute the derivative of the mse for each weight in the output layer, we need to perform two steps:- For each neuron in the output layer compute its δ
- For each weight in the output layer compute the respective partial derivative
The figure below illustrates how to compute these partial derivatives when the activation function is z = tanh(1.5y) or z = logsig(y). Observe that ti is the target for neuron i. Observe also the factor two in the computation of δ, as the derivative is used to indicate direction only, it is possible to remove this factor in the computation of δ. |